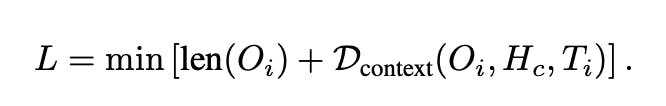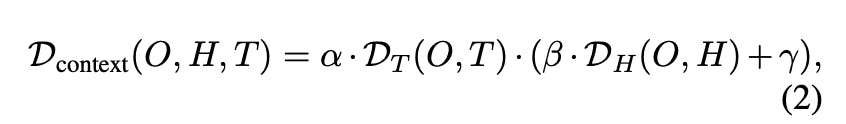New Formula Could Make AI Agents Actually Useful in the Real World

As the AI systems evolve beyond isolated features, the need for effective coordination and devoted to the context between agents powered by large language models (LLMS) is more urgent than ever. In this article, we introduce a rigorous mathematical frameworkdesignated as L functionDesigned to optimize the operation of LLM Multi-agent systems (MAS) – Dynamically, effectively and contextually.
🚀 Why we need a formal model for LLM in Mas
While the LLMS demonstrate incredible capacities in the generation of text, their Integration into Mas environments is often ad hoclacking in principle foundations to manage the context, the relevance of tasks and resource constraints. Traditional heuristics fail to evolve in real -time or high demand environments such as finance, health care or autonomous robotics.
This gap motivated the development of L function – a unifying mathematical construction for quantify and minimize ineffectiveness in LLM outputs by balancing brevity,, contextual alignmentAnd task relevance.
📐 Formal definition of the function l
Basically, the function l is defined as:
Latex notation:: L = \min \left[\text{len}({O}{i}) + \mathcal{D}{\text{context}}({O}{i}, {H}{c}, {T}_{i})\right]
Or:
len(O)is the length of the output generated.D_context(O, H, T)is the contextual deviation that considers:- Task alignment
- Historical alignment
- System dynamics
🧩 Decomposition D_context(O, H, T)
Latex notation:: \mathcal{D}{\text{context}}(O, H, T) = \alpha \cdot \mathcal{D}{T}(O, T) \cdot (\beta \cdot \mathcal{D}_{H}(O, H) + \gamma)
D_T(O, T)– Deviation specific to the task:- Latex notation::
\mathcal{D}_{T}(O, T) = \lambda \cdot \text{len}_{\text{optimal}}(O, T) - \text{len}(O)
D_H(O, H)– Historical deviation:- Latex notation::
\mathcal{D}_{H}(O, H) = 2 \cdot (1 - \cos(\vec{O}, \vec{H}))
α, β, γ– Adjustable parameters for weighting importance of the task, historical consistency and robustness.λ– a dynamic coefficient calculated like:- Latex notation::
\lambda- Or:
🧠 Why the similarity of the Cosinus?
The similarity of the Cosinus is chosen for D_H Due to sound:
-
Semantic interpretability in large spaces.
-
Invariance on a scaleAvoid distortion of vector magnitude.
-
Computer efficiency and geometric coherence.
💡 Case of use of the MAS function
1 and 1 Autonomous systems
- Context: Autonomous fleets or swarms of drones.
- The function utility: Prioritizes critical tasks such as avoidance of obstacles based on the data of the historic environment and the urgency of the mission.
2 Health decision -making
- Context: Emergency sorting systems.
- The function utility: Ensures that the historical data of patients is weighed appropriately while generating brief and precise medical responses.
3 and 3 Customer support automation
- Context: Treat thousands of tickets at different importance levels.
- The function utility: Dynamically reduces verbity for low priority tasks while preserving details in urgent interactions.
📊 Experimental results: L in action
Specific defect in the task (D_T))
- Facility: 50 synthetic tasks with variable optimal response lengths.
- Result: Tasks with
len(O)nearlen_optimalminimalLProving the logic of alignment.
Deviation of the historical context (D_H))
- Observation: Increase in the size of the context window has increased the gap, confirming that The overload of historical memory introduces semantic noise.
Dynamic λ scale
- Simulation: High priority tasks in low -resource conditions have been effectively prioritized using dynamic values λ.
Github experimental benchmark:
🔧 implementation challenges
- Vector quality sensitivity: Low quality interests are biased
D_H. PCA or normalization pretection is recommended. - Noisy historical context: Requires disintegration strategies to reduce obsolete data.
- Static parameters: Consider strengthening learning of automatic reduction
α, β, γ.
📈 Advantages of the adoption of the function L
|
Property |
Impact |
|---|---|
|
Contextual |
Semantic alignment with history and tasks |
|
Response efficiency |
Shorter and relevant outputs to reduce calculation time |
|
Adaptive prioritization |
Adjusts according to the emergency, load and resources states |
|
Agnostic domain design |
Applicable in all health care, finance, robotics |
🧪 What is the next step?
Future orientations include:
- Integrate learning to strengthen For self-relocation parameters.
- Real world deployment In distributed Mas environments.
- Robust noise integration models for better
D_Hbehavior.
📄 Mathematical and applied foundations of the function l
This article presents the fundamental principles of L function To optimize large languages models in multi-agent systems. For a complete and rigorous exhibition - including all theoretical derivations, mathematical evidence, experimental results and details of the implementation - you can refer to the complete monograph:
📘 Title:: Mathematical framework for models of large languages in multi-agent systems for interaction and optimization
Author: Raman Marozau
🔗 Access here: https://doi.org/10.36227/techrxiv.174612312.28926018/v1
If you are interested in the complete theoretical foundation and how to apply this model in production systems, we strongly recommend that you study the manuscript in detail.
☝️Conclusion
The function l presents a novel Optimization paradigm which allows LLMS to function as smart agents Rather than passive generators. By quantifying alignment and adaptation in real time, this framework employs the masters with contextual intelligence, operational efficiencyAnd Evolutionary task management - Characteristics of the next generation of AI systems.
"Optimization is not only a question of speed - it is to know what matters, when."
For collaboration or deployment requests, do not hesitate to contact you.